Muestras aleatorias y Estadísticos

Las variables aleatorias $X_1,X_2,\dots ,X_n$ constituirán una muestra aleatoria de la población $f(x)$ con valores numéricos $x_1,x_2,\dots ,x_n$ si las mediciones se obtienen repitiendo el experimento $n$ veces.

Definición de muestra aleatoria

Sea $X$ una variable aleatoria con cierta distribución de probabilidades. Sean $X_1,X_2,\dots ,X_n$, $n$ variables aletorias independientes con una con la misma distribución de $X$. Llamamos entonces, a $(X_1,X_2,\dots ,X_n)$ muestra aleatoria de la variable aleatoria $X$

Estadístico

Definición de estadístico

Cualquier función de las variables aleatorias que constituye una muestra aleatoria se llama estadístico. Sea $X_1,X_2,\dots ,X_n$ muestra aleatoria, un estadístico $T$ es cualquier función de la muestra aleatoria, es decir $T=g(X_1,X_2,\dots ,X_n)$

• Expresión matemática que depende de la muestra.

Estimador

• Expresión matemática que depende de la muestra y que no involucra a ningún parámetro.
• Solemos utilizar el estimador para conectarlo con el parámetro que quiero estimar.
• Estos estimadores tienen distribuciones.i

Tendencia central de la muestra

• Algunos estimadores más utilizados:

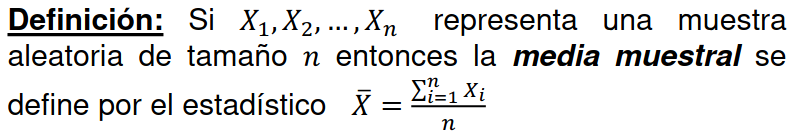
Variabilidad de la muestra

• Rango

• Varianza muestral

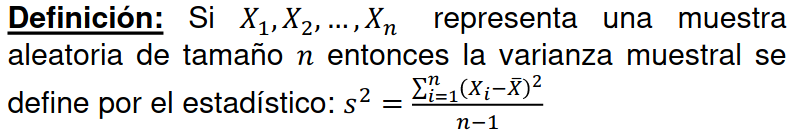
• Teorema

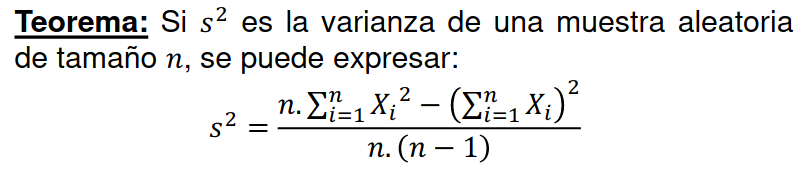
Distribución muestral del estadístico

Distribución muestral

La distribución muestral e un estadístico recibe el nombre de distribución muestral

• La distribución de probabilidad de $\bar{X}$ recibe el nombre de distribución muestral de la media.
• La distribución muestral de un estadístico depende del tamaño de la población, del tamaño de las muestras y del método de selección de estas últimas.

Teorema

Si $X_1,X_2,\dots ,X_n$ son variables aleatorias independientes que tienen distribuciones normales con medias ${\mu }_1,{\mu }_2,\dots ,{\mu }_n$ y varianzas ${\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_n^2$ respectivamente, entonces la variable aleatoria $Y=a_1{X}_1+a_2{X}_2+\cdots +a_n{X}_n$ tiene una distribución normal con media ${\mu }_Y=a_1{\mu }_1+a_2{\mu }_2+\cdots +a_n{\mu }_n$ y varianza ${\sigma }_Y=a_1^2{\sigma }_1^2+a_2^2{\sigma }_2^2+\cdots +a_n^2{\sigma }_n^2$

---

Flashcards