Estimación

Estimación puntual

• Una estimación puntual de algún parámetro poblacional $\theta$ es un valor único asumido por un estimador $\hat{\theta }$ cuando se evalúan en los valores obtenidos por una muestra particular.
  • En pocas palabras, es un número con el cual yo aproximo.
  • Posee un $\pm$ Error Estándar
    • Es el desvío estándar del estimador.
• Cuando se aproxima un parámetro de una distribución a través de un valor decimos que se está haciendo una estimación puntual.
• La calidad de la estimación obtenida depende de la adecuada elección del estimador puntual. Debido a que existe una gran variedad de estimadores posibles en cada situación particular es que necesitamos de un criterio de selección.

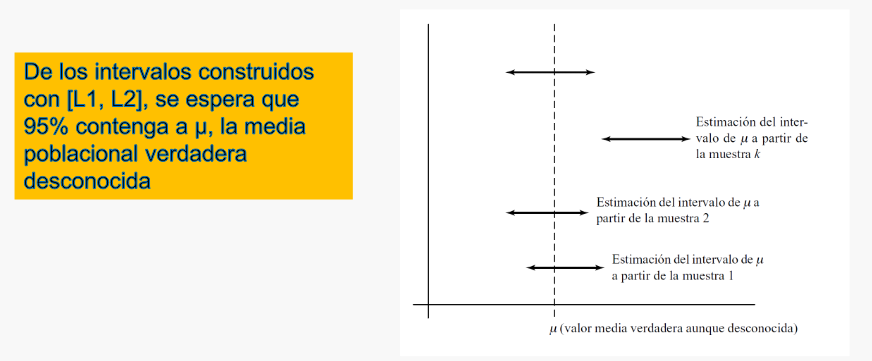
Estimación por intervalos de confianza

• Una estimación está acompañada de una posible medida de error de esa estimación. Esto se puede hacer indicando el error estándar del estimador o dando un intervalo que incluya el verdadero valor del parámetro con un cierto nivel de confianza.
• El procedimiento que permite calcular los límites superior e inferior del intervalo antedicho se conoce como: estimación por intervalo y al intervalo obtenido: Intervalo de Confianza.

Definición por intervalo

Una estimación por intervalo de un parámetro poblacional $\theta$ es un intervalo aleatorio construido de tal manera que la probabilidad de contener al parámetro sea de $1-\alpha$, es decir $P(LI\le \theta \le LS)=1-\alpha$, para $0<\alpha <1$

Método general para obtener intervalos de confianza

• Existe una función continua (estadístico) que relaciona el parámetro $\theta$ y su estimador $\hat{\theta }$, esto es $g(\theta ,\hat{\theta })$
• La función $g(\theta ,\hat{\theta })$ tiene una distribución $f$ cuya especificación (o forma funcional) no dependa del parámetro $\theta$
• Esta función $g(\theta ,\hat{\theta })$ se denomina pivote
• $g(\theta ,\hat{\theta })$ es el estadístico que relaciona el parámetro y a su estimador, y $f$ es su función de distribución.
  • $P(q_1\le g(\theta ,\hat{\theta })\le q_2=1-\alpha$
  • Una vez determinado q1 y q2, los límites LI y LS surgen despejando $\theta$ a partir de $g(\theta ,\hat{\theta })$

Estimación por IC de la media si no se conoce ${\sigma }^2$

Estimación de la diferencia entre medias si se conocen las varianzas

---

Flashcards