Métodos de Ordenamiento Iterativos

• Date::
• Course:: Estructuras de Datos II
• Source:: Métodos de Ordenamiento

Métodos de Ordenamiento

• Qué es una clave?

  • Clave: La parte de un registro por la cual se ordena la lista. Por ejemplo, una lista de registros con campos nombre, dirección y teléfono se puede ordenar alfabéticamente de acuerdo al nombre. En este caso los campos dirección y teléfono no se toman en cuenta en el ordenamiento.

• Qué es un criterio de ordenamiento o de comparación?

  • Criterio de ordenamiento o de comparación: El criterio que utilizamos para asignar orden a los registros con base en una o más claves. De esta manera decidimos si un registro es mayor o menor que otro.

• Qué es un registro?

  • Registro: Un grupo de datos que forman la lista. Pueden ser datos primitivos enteros, caracteres, reales, etc., o grupos de ellos.

• Qué es algoritmos de ordenamiento interno?

  • Son aquellos en los que los valores a ordenar están en memoria principal, por lo que se asume que el tiempo que se requiere para acceder a cualquier elemento sea el mismo (a[1], a[500], etc).
  • Vamos a utilizar la memoria interna, por lo que será una ejecución más rápida.

• Cómo se clasifican los algoritmos de ordenamiento interno?

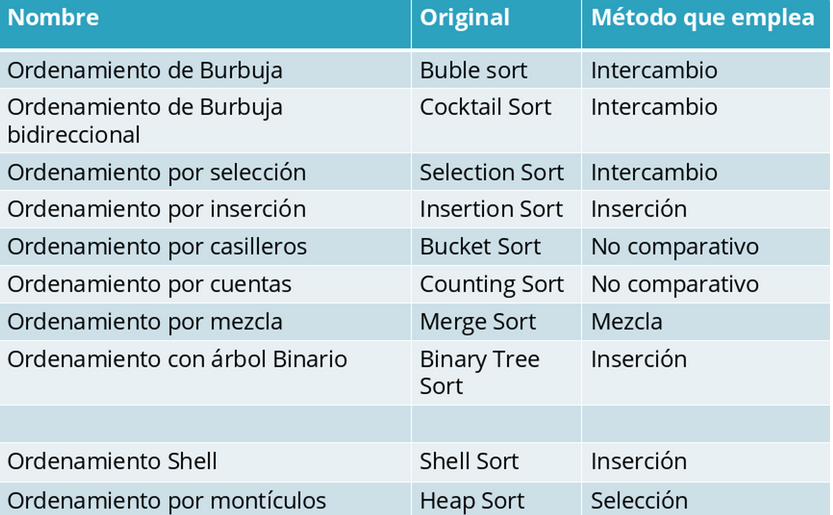
  • Algoritmos de intercambio.
  • Algoritmos de inserción.
  • Algoritmos de selección.
  • Algoritmos de enumeración.

• En qué consisten los algoritmos de intercambio?

  En este tipo de algoritmos se toman los elementos de dos en dos, se comparan y se INTERCAMBIAN si no están en el orden adecuado. Este proceso se repite hasta que se ha analizado todo el conjunto de elementos y ya no hay intercambios.

  Entre estos algoritmos se encuentran el BURBUJA y QUICK SORT.

• En qué consisten los algoritmos de inserción?

  En este tipo de algoritmo los elementos que van a ser ordenados son considerados uno a la vez. Cada elemento es INSERTADO en la posición apropiada con respecto al resto de los elementos ya ordenados.

  Entre estos algoritmos se encuentran el de INSERCION DIRECTA, SHELL SORT, INSERCION BINARIA y HASHING.

• En qué consisten los algoritmos de selección?

  En este tipo de algoritmos se SELECCIONA o se busca el elemento más pequeño (o más grande) de todo el conjunto de elementos y se coloca en su posición adecuada. Este proceso se repite para el resto de los elementos hasta que todos son analizados.

  Entre estos algoritmos se encuentra el de SELECCION DIRECTA.

• En qué consisten los algoritmos de enumeración?

  En este tipo de algoritmos cada elemento es comparado contra los demás. En la comparación se cuenta cuántos elementos son más pequeños que el elemento que se está analizando, generando así una ENUMERACIÓN. El número generado para cada elemento indicará su posición.

• Caracterice el método de la burbuja.

  Bubble sort in 2 minutes

  • Se recorre el arreglo intercambiando los elementos adyacentes que estén desordenados. Se recorre el arreglo tantas veces hasta que ya no haya cambios. Prácticamente lo que hace es tomar el elemento mayor y va recorriendo de posición en posición hasta ponerlo en su lugar. Es preciso señalar que es quizás el método más ineficiente.

  • El método de intercambio directo puede trabajar de dos maneras diferentes: llevando los elementos más pequeños hacia la parte izquierda del arreglo o trasladando elementos más grandes hacia su parte derecha. La idea básica de este algoritmo consiste en comparar pares de elementos adyacentes e intercambiarlos entre si hasta que los elementos se encuentren ordenados.

    • En el peor de los casos se realizan (n - 1) pasadas transportando en cada una  el elemento de menor o mayor  —según sea el caso— a su position ideal. Al final  (n - 1) pasadas los elementos del arreglo estarán ordenados.

  • El número de comparaciones que se realizan en el método de la burbuja se puede contabilizar fácilmente.

  • En la primera pasada se realizan (n - 1) comparaciones, en la segunda pasada (n -2) comparaciones, en la tercera pasada (n - 3) comparaciones y así sucesivamente hasta llegar a 2 y 1 comparaciones entre claves, siendo n el número de elementos del arreglo. Por lo tanto, tenemos que el numero de comparaciones es:

    $$C=(n-1)+(n-2)+\cdots +2+1=\frac{n(n-1)}{2}=\frac{n^2-n}{2}$$

• Caracterice el método de baraja (inserción directa).

  Insertion sort in 2 minutes

  • La idea central de este algoritmo consiste en insertar un elemento del arreglo en la parte izquierda del mismo, que ya se encuentra ordenada. Este proceso se repite desde el segundo hasta el n-esimo elemento.
  • En este método se considera que en todo momento se tiene la secuencia de elementos a ordenar dividida en dos subsecuencias, la primera de ellas, A(1), A(2), .. ,A(i-1) ya ordenada, y la segunda, A(i), .. ,A(n), con los elementos que faltan por ordenar. En cada paso, empezando con i=2, e incrementando el valor de i de uno en uno, se toma el elemento i del array y se inserta en el sitio adecuado dentro de la subsecuencia ordenada. El caso i=1 no se tiene en cuenta pues se considera que el primer elemento esta ordenado respecto a si mismo.
  • Cuando se considera el segundo elemento (i=2) se trata de ubicarlo corréctamente respecto a lo que ya esta ordenado (un único elemento), lo que implica simplemente una comparación. A medida que el tamaño de la subsecuencia ordenada aumenta, se incrementa el número de comparaciones necesarias para insertar un elemento. La inserción de cada elemento implica ir comparando y desplazando secuencialmente un elemento respecto a todos los anteriores hasta encontrar su posición correcta en el array.
  • El criterio de finalización del proceso de inserción de un elemento es doble: que se encuentre un elemento con clave menor que el que se desea insertar (suponiendo comparaciones desde el final de la secuencia ordenada) o bien, que se llegue al principio de la secuencia sin encontrar ningún elemento menor. En cuyo caso la posición correcta del elemento será la primera.

• Caracterice el método de selección.

  Selection sort in 3 minutes

  • El método de ordenamiento por selección consiste en encontrar el menor de todos los elementos del arreglo e intercambiarlo con el que está en la primera posición. Luego el segundo mas pequeño, y así sucesivamente hasta ordenar todo el arreglo.

• Caracterice el método Shell Shell Sort (ordenamiento)

  • Shell nos propone que hagamos sobre el arreglo una serie de ordenaciones basadas en la inserción directa, pero dividiendo el arreglo original en varios sub-arreglos tales que cada elemento esté separado K elementos del anterior (a esta separación a menudo se le llama salto o gap)
  • Se debe empezar con k=n/2, siendo n el número de elementos de arreglo, y utilizando siempre la división entera.
  • Después iremos variando k haciéndolo mas pequeño mediante sucesivas divisiones por 2, hasta llegar a k=1.
  • En cuanto al estudio de su complejidad, este método es diferente al resto de los procedimientos vistos en esta unidad. Su complejidad es difícil de calcular y depende mucho de la secuencia de incrementos que utilice. Por ejemplo, para la secuencia dada existen dos conjeturas en cuanto a su orden de complejidad: nlog²n y n1.25.
  • En general este método es el escogido para muchas aplicaciones reales por ser muy simple teniendo un tiempo de ejecución aceptable incluso para grandes valores de n.