Tipos de redes estáticas
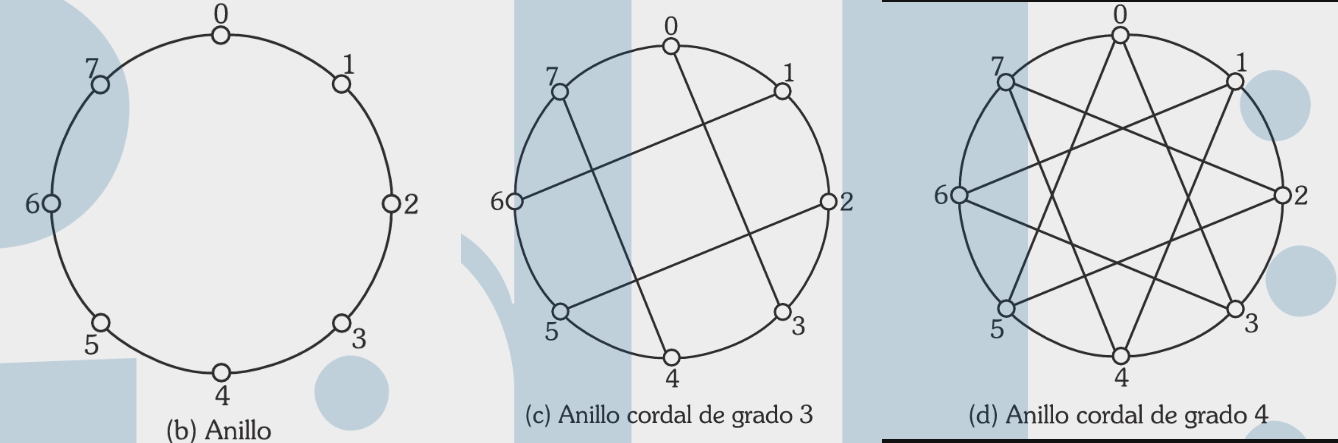
Formación lineal
En esta topología, los N nodos se conectan cada uno con el siguiente mediante N-1 enlaces, formando una línea. Los nodos interiores tienen grado 2 y los extremos tienen grado 1. El diámetro de esta red es N-1 y su ancho de bisección es 1. Es la estructura más sencilla, pero no es regular y puede ser ineficiente para valores altos de N.
- Puede ser muy eficiente porque si tengo mucha distancia entre los nodos finales, la información debe transmitirse por todos los nodos.
Anillo y anillo cordal
Una red en anillo se obtiene conectando entre sí los nodos extremos de una formación lineal. Todos los nodos tienen grado 2 y el diámetro es N/2. Si los enlaces son unidireccionales, el diámetro sería N-1. El anillo cordal aumenta el grado de los nodos a 3 o 4, reduciendo así el diámetro. El caso más extremo es la red totalmente conectada, donde cada nodo está conectado a todos los demás.
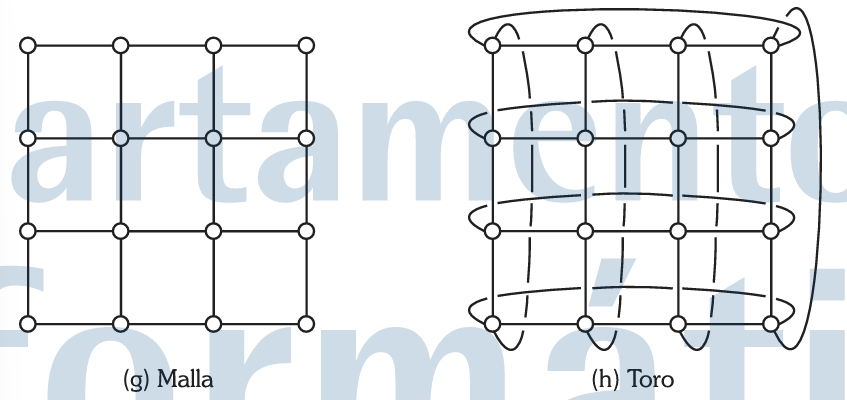
Mallas y toros
Una malla k-dimensional tiene lk nodos, donde l es el número de nodos por lado. El grado de los nodos varía entre k para los vértices y 2k para los nodos interiores. El diámetro es k(l-1). Las redes en toro son mallas donde las filas y columnas tienen conexiones en anillo, lo que reduce su diámetro a la mitad.
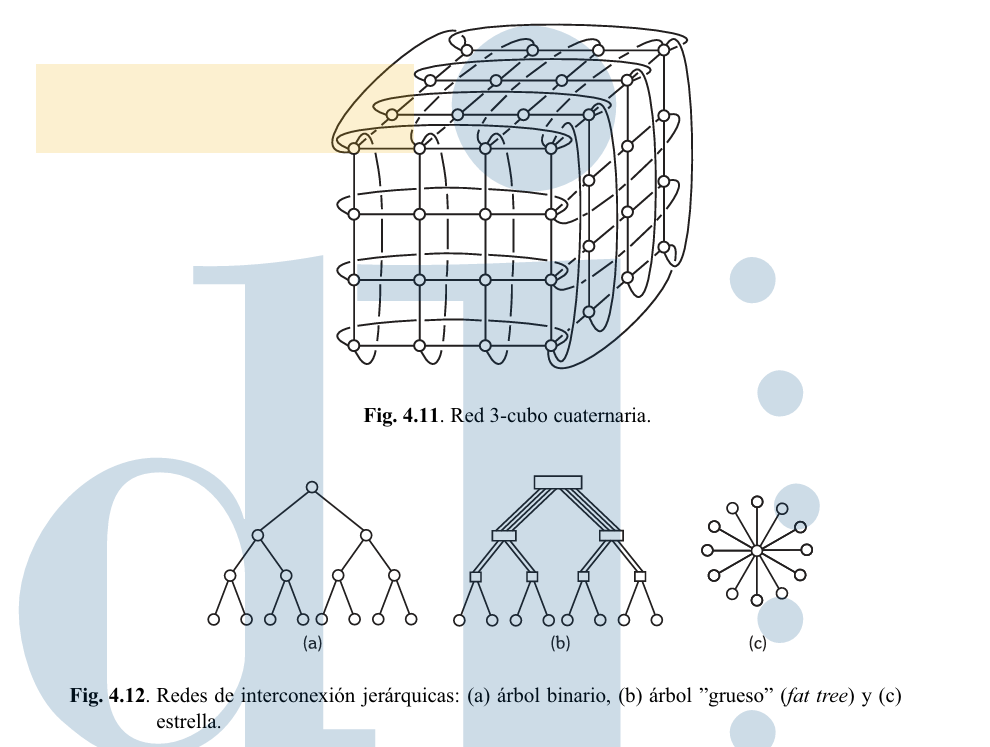
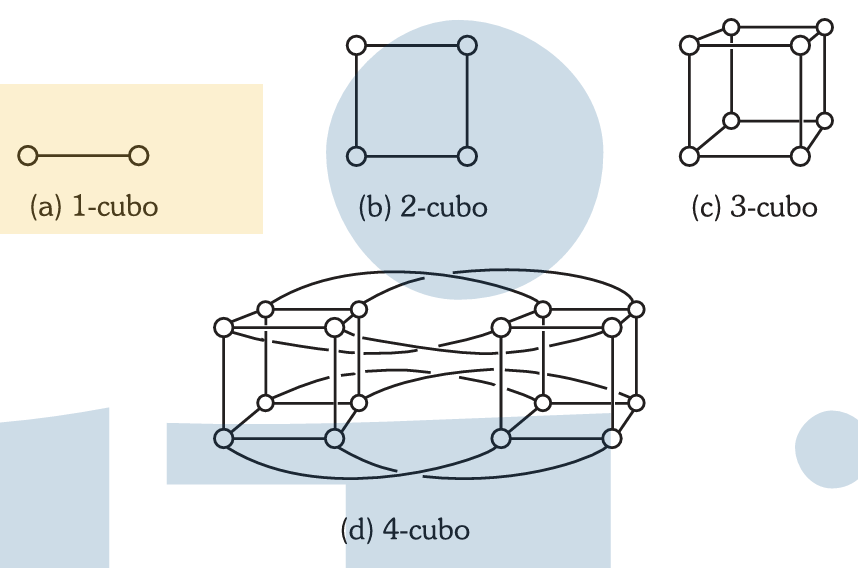
Hipercubo
Un hipercubo n-dimensional tiene 2^n nodos, donde cada nodo está conectado a n nodos adyacentes. El grado de los nodos es n, lo que dificulta la escalabilidad de esta topología.
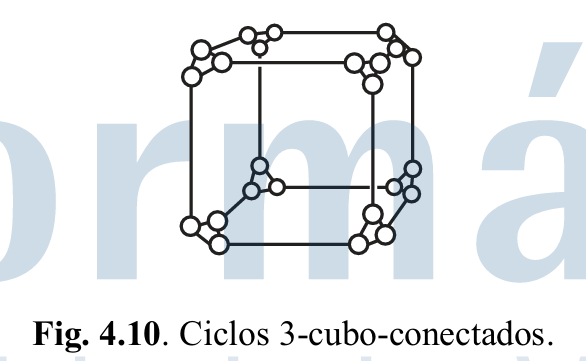
Ciclos hipercubo-conectados
En esta red, cada vértice del hipercubo se sustituye por un anillo de n nodos. Así, el número de nodos aumenta a n*2^n y el diámetro a 2n. Todos los nodos tienen grado 3, lo que mejora la escalabilidad.
n-cubos k-arios
Esta topología generaliza algunas de las anteriores. Consiste en un cubo n-dimensional con k nodos a lo largo de cada dimensión, donde todas las aristas tienen estructura de anillo. Los anillos, toros e hipercubos son casos particulares de esta red.
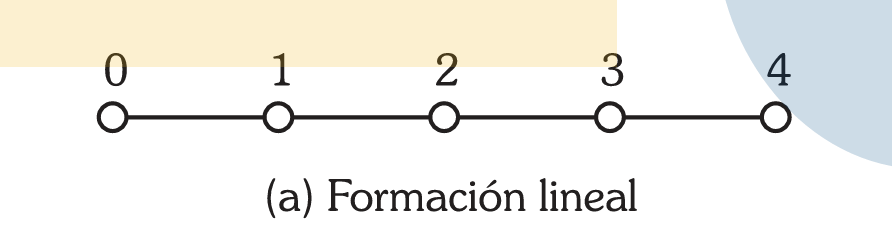
Topologías jerárquicas
El ejemplo más extremo es el árbol binario equilibrado de k niveles, con 2^k-1 nodos. El grado de los nodos es 3 (excepto raíz y hojas) y el diámetro es 2(k-1). Una variante es el árbol grueso, donde los nodos interiores son conmutadores en lugar de elementos de proceso.